3  Regular time series

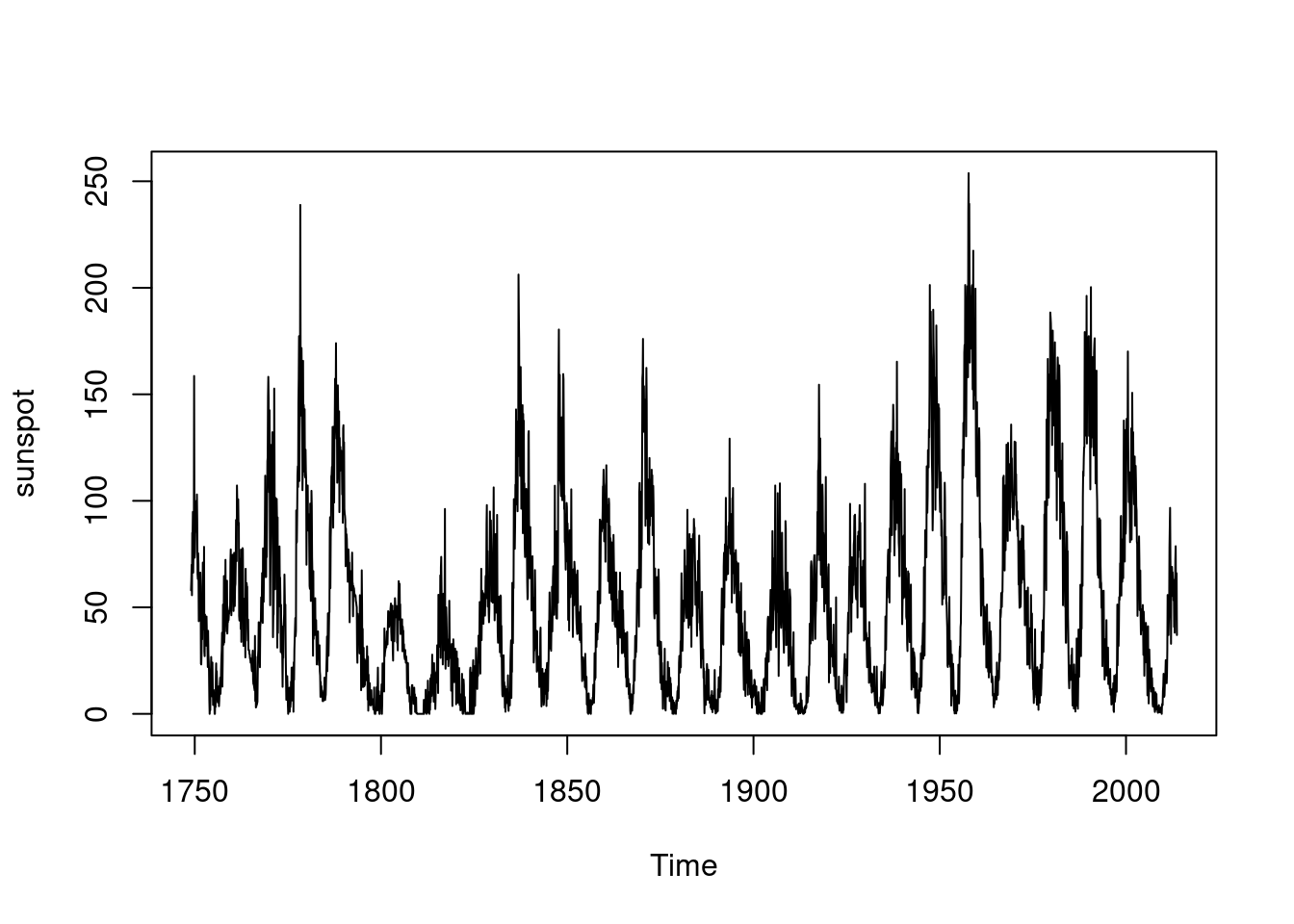
If a time series is “regular”, that is it has equal time steps between observations, and no missing observations, then its power spectrum can be estimated from its Fourier transform.

3.1 The Fourier Transform

sunspot <- datasets::sunspot.month
plot(sunspot)

library(PaleoSpec)
sp_sun <- SpecMTM(sunspot)
LPlot(sp_sun)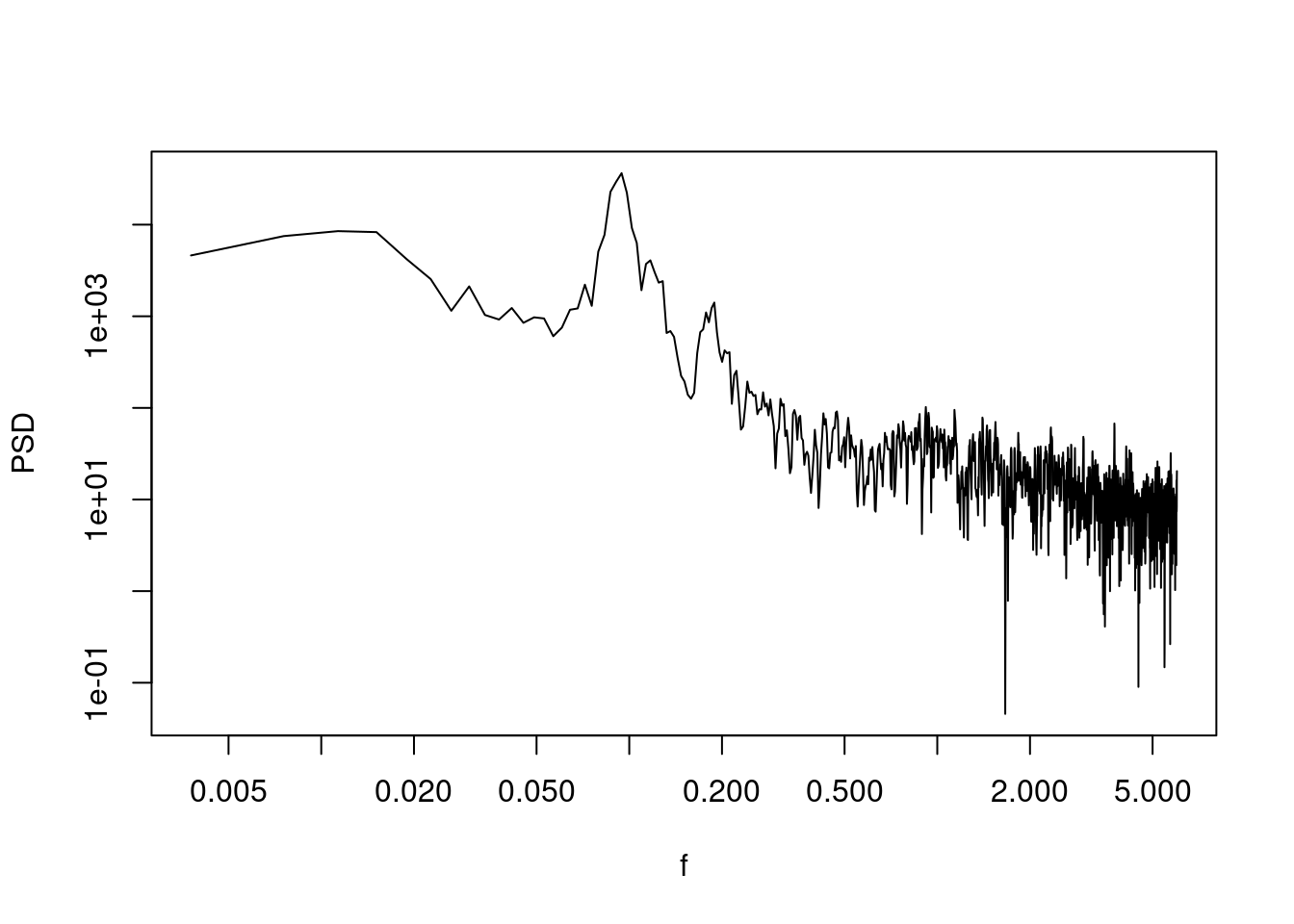

3.2 The Multitaper Method

3.3 To detrend or not

3.3.1 Why detrend?

library(dplyr)

Attaching package: 'dplyr'

The following objects are masked from 'package:stats':

    filter, lag

The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union

library(tidyr)
library(PaleoSpec)
library(ggplot2)

f1 <- 1/10
f2 <- 1/100
f3 <- 1/1000

tau <- 1e04

#tau / (1/c(f1, f2, f3))

dat <- tibble(
  time = seq(0, tau, by = 1),
  y = cos(2*pi*f1*time) + cos(2*pi*f2*time) + cos(2*pi*f3*time) 
) %>% 
  mutate(y = y + rnorm(n(), 0, 0.1))

plot(dat$time, dat$y, type = "l")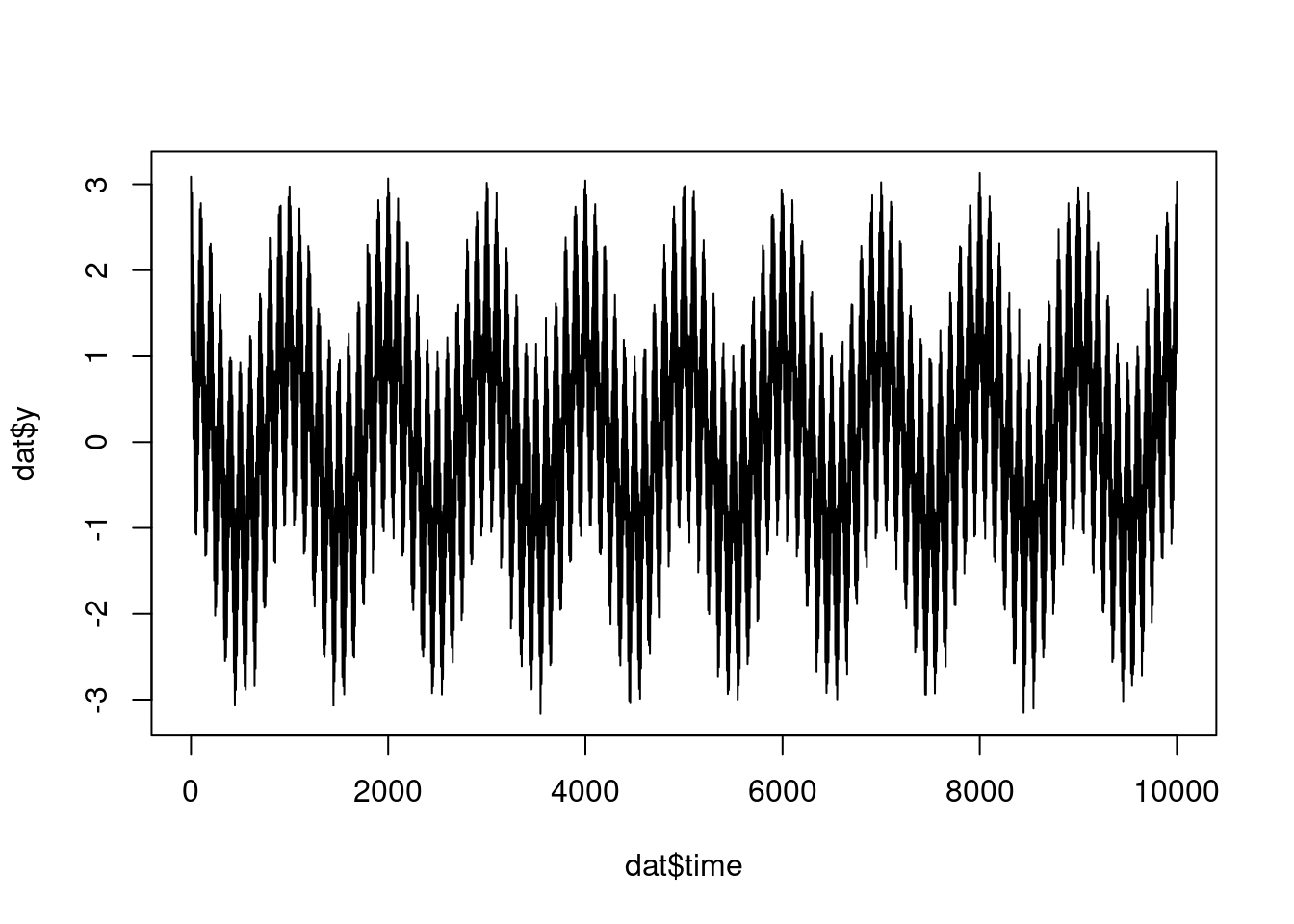

sp1 <- SpecMTM(ts(dat$y, deltat = 1), detrend =  FALSE)
sp1_detr <- SpecMTM(ts(dat$y, deltat = 1), detrend =  TRUE)

#sp1 <- SpecACF(ts(dat$y, deltat = 1), bin.width = 1, detrend =  FALSE)


gg_spec(list(sp1, detrended = sp1_detr)) +
  geom_vline(xintercept = c(f1, f2, f3), lty = 2, colour =  "Red")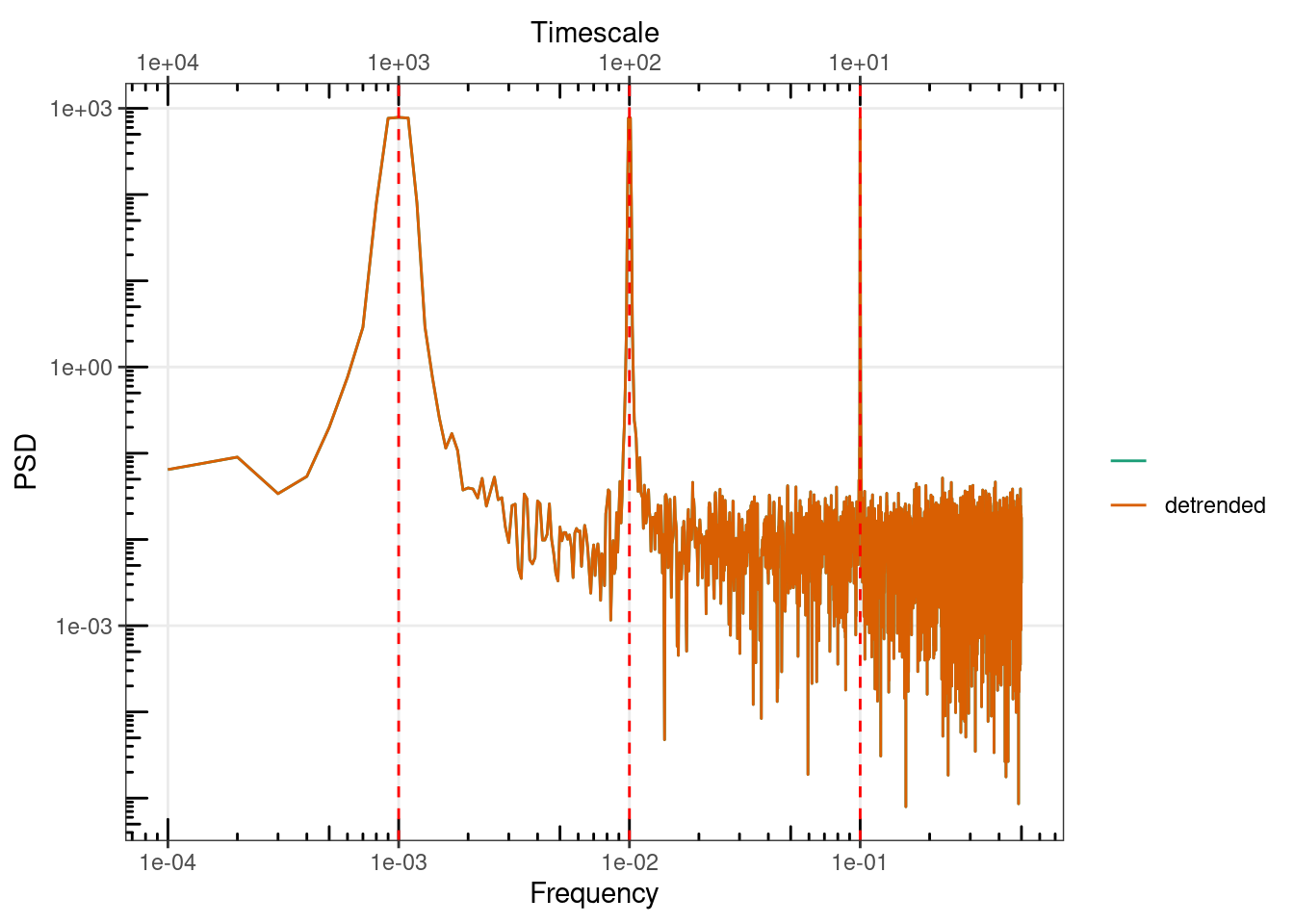

sp1_10k <- SpecACF(ts(dat$y, deltat = 1), bin.width = 1, detrend =  FALSE)
sp1_10k_detr <- SpecACF(ts(dat$y, deltat = 1), bin.width = 1, detrend =  TRUE)

plot(y~time, data = dat[1:500,],  type = "l")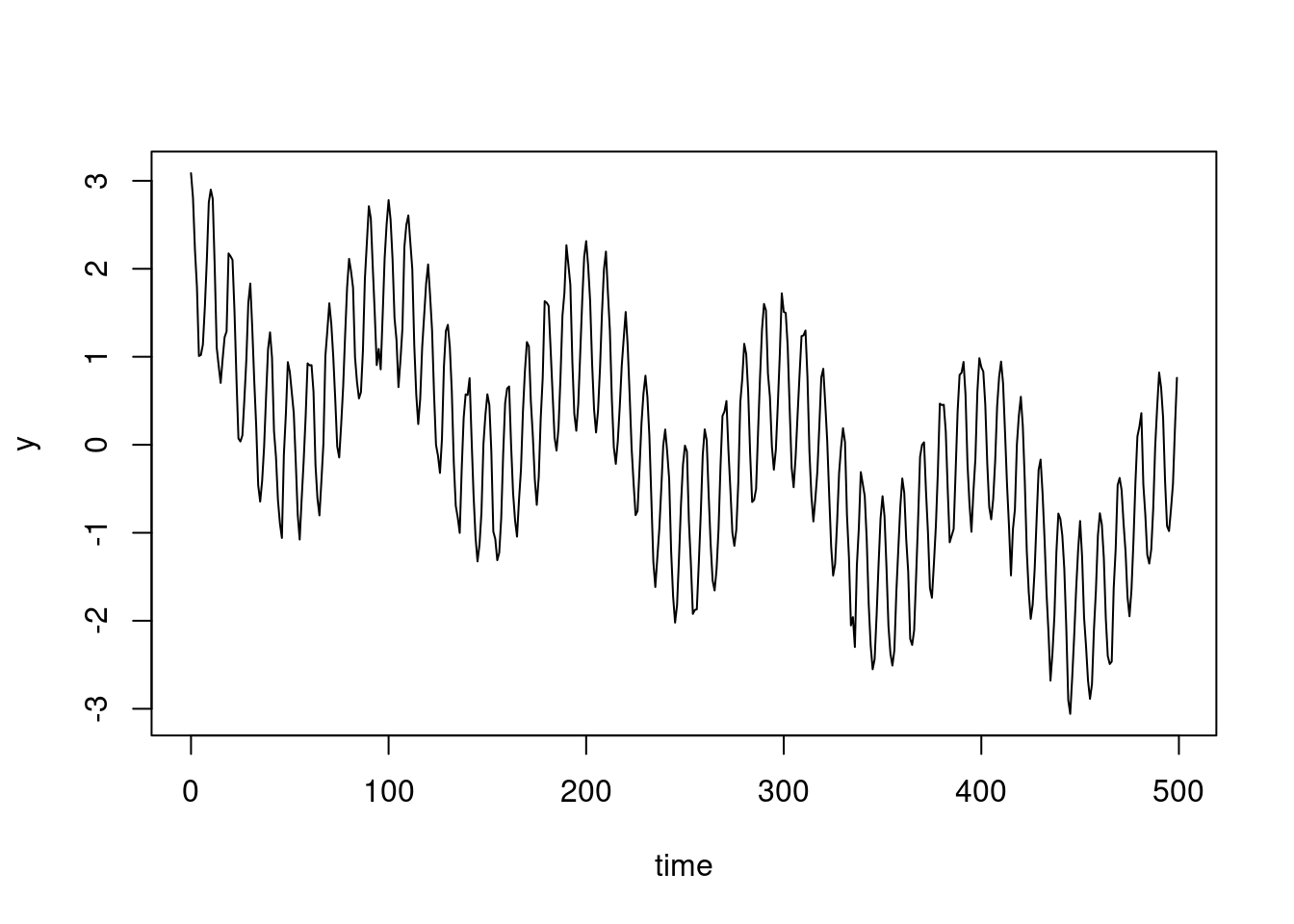

sp1_0.5k <- SpecACF(ts(dat$y[1:500], deltat = 1), bin.width = 1, detrend =  FALSE)
sp1_0.5k_detr <- SpecACF(ts(dat$y[1:500], deltat = 1), bin.width = 1, detrend =  TRUE)


sp1_0.5k_detr_MTM <- SpecMTM(ts(dat$y[1:500], deltat = 1), detrend =  TRUE)


list(
  raw_10k = (sp1_10k),
  detrended_10k = (sp1_10k_detr),
  raw_0.5k = (sp1_0.5k), 
  detrended_0.5k = (sp1_0.5k_detr)
  #detrended_0.5k_MTM = (sp1_0.5k_detr_MTM)
  ) %>% 
  lapply(., Spec2DF) %>% 
  bind_rows(., .id = "name") %>% 
  separate(name, into = c("detrended", "length"), sep = "_") %>% 
  mutate(spec_id = detrended) %>% 
  as_spec_df() %>% 
  gg_spec(., colour = detrended) +
  facet_wrap(~length)#+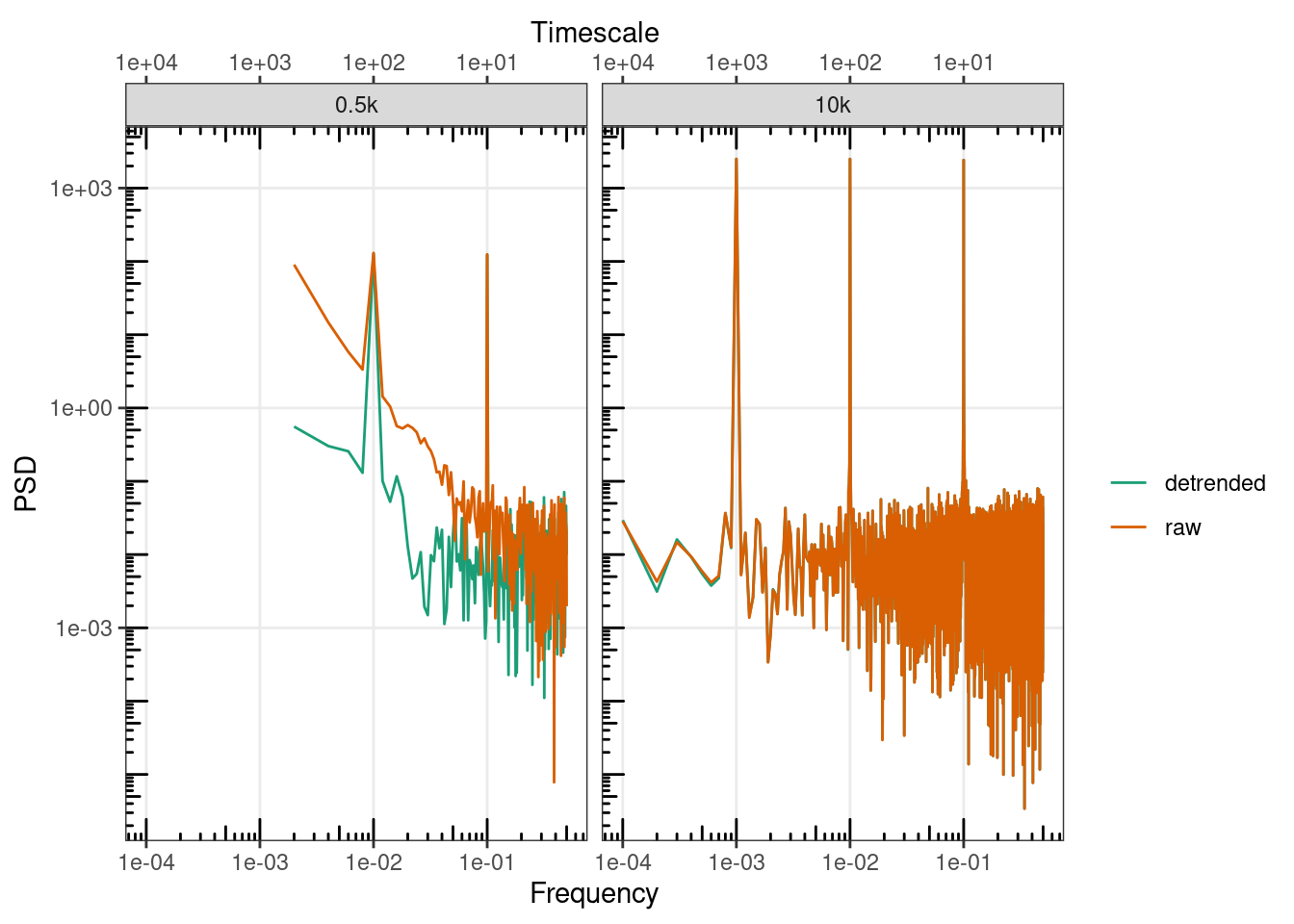

  #geom_vline(xintercept = c(f1, f2, f3), lty = 2, colour =  "blue")

• Even with detrend = FALSE, SpecMTM does some detrending - must be part of the tapering?

library(dplyr)
library(tidyr)
library(PaleoSpec)
library(ggplot2)


N <- 1e03
n_rep <- 1000
alpha = 0.1
beta = 0

dat <- crossing(
  rep = 1:n_rep,
  t = 1:N
) #%>% 
  # group_by(rep) %>% 
  # mutate(
  #   y = PaleoSpec::SimPLS(N = N, beta = beta, alpha = alpha) 
  # )

# Get a matrix of simulated timeseries
ts_m <- replicate(n_rep, PaleoSpec::SimPLS(N = N, beta = beta, alpha = alpha))

mean_spec <- SpecACF(ts_m, bin.width = 1, detrend = FALSE)
mean_spec_detrended <- SpecACF(ts_m, bin.width = 1)

dat$y <- as.numeric(ts_m)

specs_mtm_detrend <- dat %>% 
  group_by(rep) %>% 
  do({
    Spec2DF(SpecMTM(ts(.$y), 
                    detrend = TRUE
                    )
            )
  })

specs_mtm_raw <- dat %>% 
  group_by(rep) %>% 
  do({
    Spec2DF(SpecMTM(ts(.$y), 
                    detrend = FALSE
                    )
            )
  })


mean_spec_MTM_raw <- specs_mtm_raw %>% 
  group_by(freq) %>% 
  summarise_if(is.numeric, mean)

mean_spec_MTM_detrended <- specs_mtm_detrend %>% 
  group_by(freq) %>% 
  summarise_if(is.numeric, mean)

gg_spec(list("Periodogram_raw_ts" = mean_spec,
             "Periodogram_detrended_ts" = mean_spec_detrended,
             MTM_detrended = mean_spec_MTM_detrended,
             MTM_raw_ts = mean_spec_MTM_raw)) #+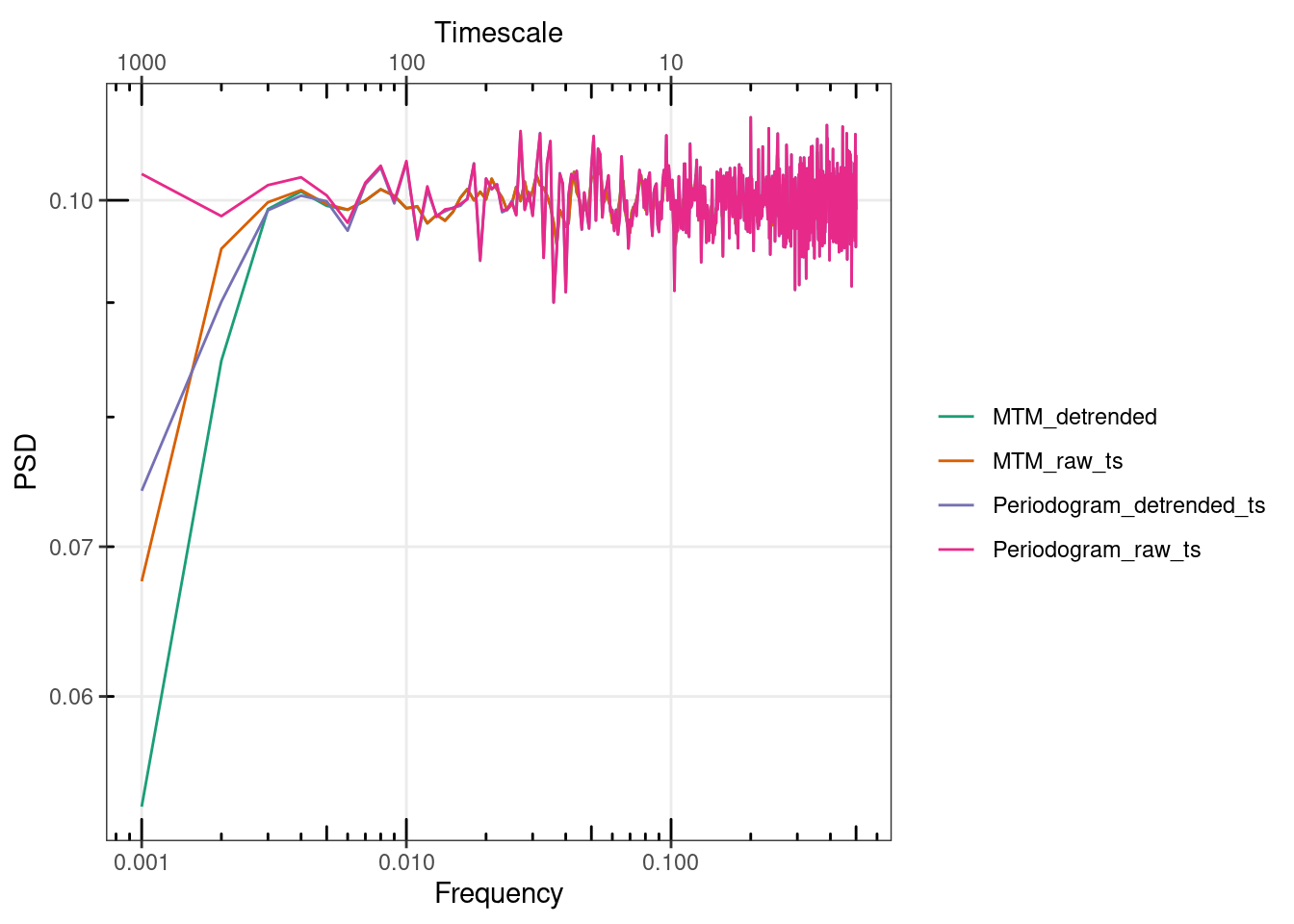

  #geom_point(aes(x = freq, y = spec, colour = spec_id))

3.4 Errors

• Explain Gamma / Chi-Sq nature of the errors
• Degrees of freedom / shape of Gamma
• Effect of tapering and smoothing on error distribution
• Confidence intervals