Add confidence interval

Calculated confidence intervals give the interval within which the true spectrum should lie with frequency 1-p. This behaviour changed with version 0.33.

Previous versions returned the interval which, when applied to the 'true' spectrum, would contain new spectral estimates with frequency 1-p.

Usage

AddConfInterval(spec, pval = 0.05, MINVALUE = 1e-10)

Arguments

spec

a spectral object of class "spec" or a list with the minimum components spec and dof which are vectors of the same length giving the spectral estimates and the corresponding degrees of freedom.

pval

numeric; p value for the confidence interval, i.e. the interval is constructed from pval / 2 to 1 - pval / 2.

MINVALUE

numeric; minimum value to limit the confidence interval.

Value

the input object including the new list elements lim.1 and lim.2 giving the upper and lower bound of the confidence interval, respectively.

Details

Add a confidence interval to a spectral estimate assuming the uncertainty of the spectral estimates follows a chi-squared distribution with the degrees of the freedom from the spectral estimates.

Author

Thomas Laepple, Andrew Dolman

Examples

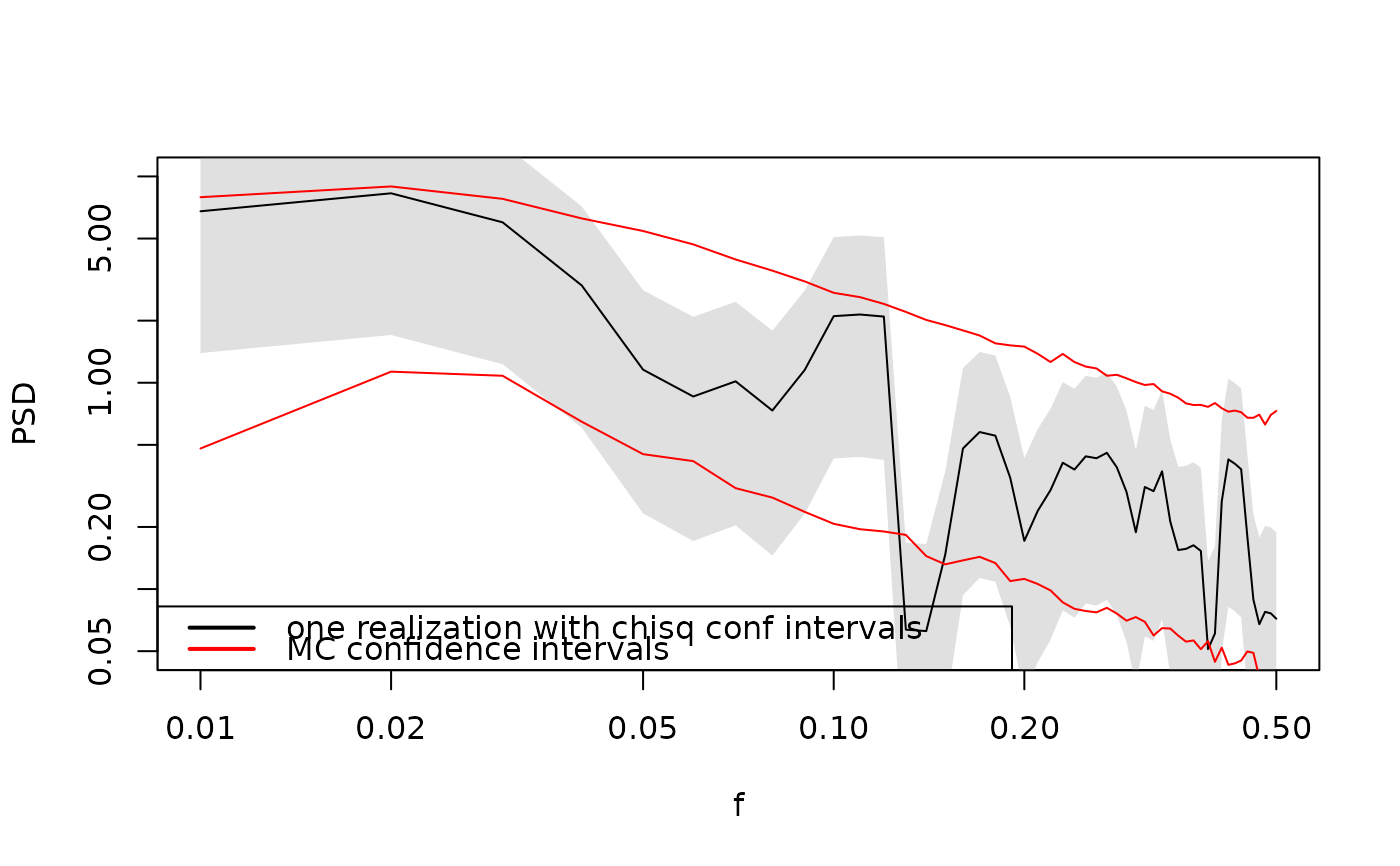
alpha <- 0.1
beta <- 1

spec_sim <- SpecMTM(ts(SimPLS(N = 1e03, beta = beta, alpha = alpha)))

# Using a large nominal p value of 0.25 to reduce variation between random
# timeseries

# The true spec should be p/2 times above the lower CI, and p/2 below the upper CI

nominal_p <- 0.25
spec_sim <- AddConfInterval(spec_sim, pval = nominal_p)
true_spec <- alpha * spec_sim$freq^-beta

LPlot(spec_sim)
abline(a = log10(alpha), b = -beta, lty = 2, col = "red")


SpecCoverage <- function(spec, true_spec){

  stopifnot("lim.1" %in% names(spec))

  n <- length(spec$freq)
  below <- sum(spec$lim.1 < true_spec)
  above <- sum(spec$lim.2 > true_spec)

  total <- below + above

  count <- list(n = n, above = above, below = below, total = total,
                p_above = above / n, p_below = below / n,
                p_total = total / n,
                nominal_pval = spec$pval)

  as.data.frame(count)
}

SpecCoverage(spec_sim, true_spec)
#>     n above below total p_above p_below p_total nominal_pval
#> 1 500    51    44    95   0.102   0.088    0.19         0.25